Lasers
EPOCH can support laser sources on the boundaries, with a wide array of spatial and temporal profiles. These examples provide basic input decks for simulating lasers in vacuum. General documentation on the EPOCH laser block can be found here.
Simple plane wave
This input deck provides the most basic form of laser. We use uniform spatial and temporal profiles, and inspect the Poynting flux in the simulation window. As a typical rule of thumb, allow 20 cells per wavelength to get a good resolution.
begin:control
nx = 200
ny = 400
t_end = 100e-15
x_min = 0
x_max = 10e-6
y_min = -10e-6
y_max = 10e-6
stdout_frequency = 100
end:control
begin:boundaries
bc_x_min = simple_laser
bc_x_max = open
bc_y_min = open
bc_y_max = open
end:boundaries
begin:laser
boundary = x_min
intensity_w_cm2 = 1.0e18
lambda = 1.0e-6
end:laser
begin:output
dt_snapshot = 10 * femto
poynt_flux = always
end:output

As we have specified a time-averaged intensity of $10^{18} \text{ Wcm}^{-2}$, we expect the Poytning flux to range 0 to $2\times 10^{18} \text{ Wcm}^{-2}$, which we can see here. Note that, because our laser profile reaches the $y_{min}$ and $y_{max}$ boundaries, some noise has been introduced here. In practice, these boundary effects are less of an issue, as simulations are expected to mainly deal with laser pulses.
Laser pulse
Using the maths parser, we can create a laser pulse which has a Gaussian profile in time and space for the intensity distribution, $I$:
$ I(y,t) \propto e^{-(y-y_0)^2/2\sigma_y^2} e^{-(t-t_0)^2/2\sigma_t^2}$
where we consider a 2D simulation with an $x$ propagating laser.
Let the full-width-at-half-maximum of the spatial and temporal profiles be 5 $\mu m$ and 40 fs respectively for the intensity $I$ distribution. The relationship between $\sigma$ and the $fwhm$ for a Gaussian distribution is:
$\sigma = \frac{fwhm}{2\sqrt{2 \ln(2)}}$
However, the profile keys in the laser block describe modifications to the boundary electric fields, $E$, and as $I \propto E^2$, the $E$ profile must satisfy
$ E(y,t) \propto e^{-((y-y_0)/2\sigma_y)^2} e^{-((t-t_0)/2\sigma_t)^2}$
The EPOCH
maths parser provides
a special gauss(x,x_0,w) command for use in the input.deck, which sets a
profile of the form:
$e^{-(x-x_0)^2/w^2}$
Hence, we may use this gauss function to model the electric field profiles if
we set
$w = \frac{fwhm}{\sqrt{2\ln(2)}}$
where $fwhm$ refers to the intensity distribution.
We can let the spatial profile peak at $y=0$. We don’t want the laser to peak at $t=0$, as this would ignore the rising intensity. Instead, let us start when the laser pulse is 10% of its maximum value - the half-width-at-10%-maximum, $hw0.1m$. For a Gaussian beam, this is:
$hw0.1m = \frac{fwhm}{2} \sqrt{\frac{\ln(10)}{\ln(2)}}$
begin:control
nx = 700
ny = 400
t_end = 100e-15
x_min = 0
x_max = 35e-6
y_min = -10e-6
y_max = 10e-6
stdout_frequency = 100
end:control
begin:boundaries
bc_x_min = simple_laser
bc_x_max = open
bc_y_min = open
bc_y_max = open
end:boundaries
begin:constant
t_fwhm = 40.0e-15
y_fwhm = 5.0e-6
w_t = t_fwhm / sqrt(2*loge(2))
w_y = y_fwhm / sqrt(2*loge(2))
t_hw01m = 0.5 * t_fwhm * sqrt(loge(10)/loge(2))
end:constant
begin:laser
boundary = x_min
intensity_w_cm2 = 1.0e18
lambda = 1.0e-6
profile = gauss(y,0,w_y)
t_profile = gauss(time,t_hw01m,w_t)
end:laser
begin:output
dt_snapshot = 10 * femto
poynt_flux = always
end:output
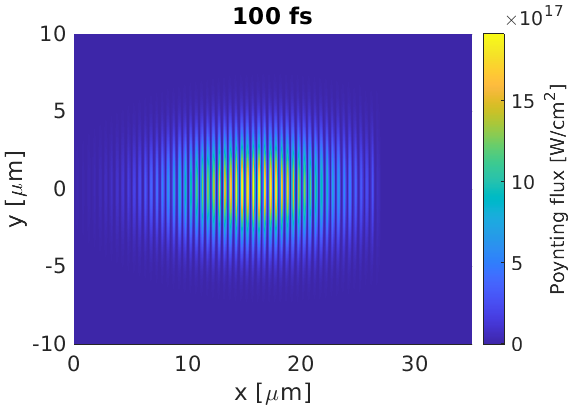
Here we see that the laser $fwhm$ in $x$ and $y$ are 12 $\mu m$ and 5 $\mu m$ respectively, where the $x$ $fwhm$ corresponds to a temporal FWHM of 40 fs, as expected. Also, because there is little contact between the pulse and the boundaries, we do not have any numerical boundary disturbance.
Angled laser pulse
A Gaussian laser pulse like the one in the previous example may be injected at
an angle into an EPOCH simulation. This is achieved by defining the spatial and
temporal laser envelopes in a rotated co-ordinate system (temporal envelope is
equivalent to an envelope in the laser-propagation direction). In this example,
the parameters y_rot and t_rot will describe the transverse and longitudinal
co-ordinates in the rotated co-ordinate system. Transformations are required
for both the profile and the phase of the laser.
EPOCH uses the provided intensity to set $B$ values parallel to the boundary -
on x_min, this sets $B_y$ and $B_z$. EPOCH sets these fields assuming the
laser travels perpendicular to the boundary, but this will over-estimate the $B$
fields in our rotated co-ordinate system, as part of the magnetic field will
also oscillate in the boundary normal direction. To correct for this, an
additional cos(theta) parameter is required for intensity in the laser
block.
Finally, we must also be careful about the time when the peak laser intensity enters the simulation. In the previous example, we set this to the half-time at 10% maximum, such that the laser started at 10% of its maximum intensity and then increased to full. In a rotated laser, the wave-front corresponding to the peak intensity arrives earlier on one of the laser edges than the other. Let us set the injection time such that this “early edge” starts at 1% of the maximum intensity. We will define the $y$ position of this “early edge” to be the half-width at 1% maximum for the spatial profile. This way, we will sufficiently model the full envelope, regardless of the injection angle.
Here we provide an input deck which specifies a point on the laser path, and an injection angle. Two constant blocks are provided: the first is for users to set laser parameters, and the second derives parameters in the rotated co-ordinate system.
begin:control
nx = 500
ny = 500
t_end = 200e-15
x_min = 0
x_max = 25e-6
y_min = 0e-6
y_max = 25e-6
stdout_frequency = 50
end:control
begin:boundaries
bc_x_min = simple_laser
bc_x_max = open
bc_y_min = open
bc_y_max = open
end:boundaries
begin:constant
t_fwhm = 40.0e-15 # Temporal FWHM
y_fwhm = 5.0e-6 # Spatial FWHM
y_foc = 5.0e-6 # y co-ord on laser path
x_foc = 10.0e-6 # x co-ord on laser path
las_theta_deg = -45 # Laser angle to boundary normal
I_peak_Wcm2 = 1.0e19 # Peak cycle-averaged intensity
las_lambda = 1.0e-6 # Laser wavelength
end:constant
begin:constant
las_theta = las_theta_deg * pi / 180.
y0 = y_foc - (x_foc - x_min) * tan(las_theta)
y_rot = y*cos(las_theta)
y0_rot = y0*cos(las_theta)
w_y = y_fwhm / sqrt(2*loge(2))
y_hw001m = 0.5 * y_fwhm * sqrt(loge(100)/loge(2)) # Half-width 1% max
w_t = t_fwhm / sqrt(2*loge(2))
t_hw001m = 0.5 * t_fwhm * sqrt(loge(100)/loge(2)) # Half-width 1% max
t_rot = time - (y-y0)*sin(las_theta)/c
t_hw001m_rot = t_hw001m + abs(y_hw001m * sin(las_theta) / c)
I_peak_rot = I_peak_Wcm2 * cos(las_theta)
end:constant
begin:laser
boundary = x_min
intensity_w_cm2 = I_peak_rot
lambda = las_lambda
profile = gauss(y_rot, y0_rot, w_y) * gauss(t_rot, t_hw001m_rot, w_t)
phase = -2 * pi * (y-y0_rot) * sin(las_theta) / las_lambda
end:laser
begin:output
dt_snapshot = t_end / 10
poynt_flux = always
end:output
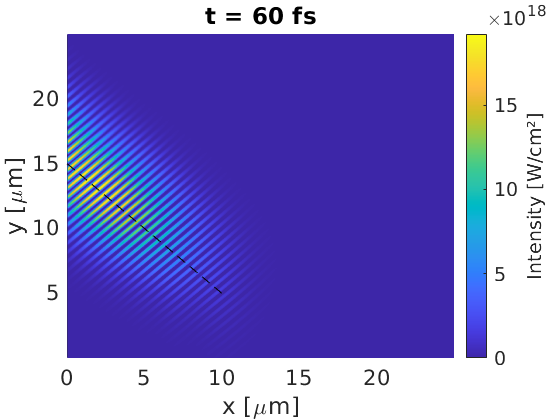
Here, we see the Poynting flux corresponds to a rotated Gaussian pulse. The expected laser trajectory is marked with a dashed line for comparison. We see that the wavelength, along with the spatial and temporal FWHM are as expected.
Focussing a Gaussian Beam
A laser can be driven on the boundary so that it focusses on a given spot. Basic details of how to do this are here. To summarise, using the paraxial approximation, the electric fields for a $x$-propagating, $y$-polarised Gaussian beam take the form:
$\pmb{E}(r,x) = E_0 \frac{w_0}{w(x)} e^{-r^2/w(x)^2} e^{-i(kx + k\frac{r^2}{2R_c(x)}-\psi(x))} \hat{\pmb{y}}$
where
- $r$ is the radial distance from the laser propagation axis
- $x$ is axial distance along the wave, with $x=0$ at the focus
- $E_0$ is the peak electric field amplitude at the focus
- $w(x)$ is the beam-waist at $x$ (radial distance where field strength drops by $e^{-1}$)
- $w_0$ is $w(x=0)$
- $k$ is the laser wave-vector
- $R_c(x)$ is the radius of curvature at $x$
- $\psi(x)$ is the Gouy phase correction
If the fields on the simulation boundary are of this form, then the fields will propagate according to this equation, and a focal spot will be formed. Note that this propagation is only expected provided the paraxial approximation is satisfied. This implies that, for vacuum propagation, the laser wavelength, $\lambda$ is much smaller than the beam-waist: $\lambda « w_0$.
The following deck gives an example for a laser attached to x_min. Two constant blocks are provided: the first gives the user control over the focused laser properties, and the second derives variables to be used in the laser block. The user only needs to touch the first, which sets the intensity full-width-at-half-maximum (related to beam-waist), the peak, cycle-averaged intensity, the laser wave-length and the distance from the $x_{min}$ boundary to the focal point.
begin:control
nx = 2400
ny = 1200
t_end = 100e-15
x_min = 0
x_max = 20e-6
y_min = -5e-6
y_max = 5e-6
stdout_frequency = 100
end:control
begin:boundaries
bc_x_min = simple_laser
bc_x_max = open
bc_y_min = open
bc_y_max = open
end:boundaries
begin:constant
I_fwhm = 2.0e-6 # FWHM of laser intensity
I_peak_Wcm2 = 1.0e15 # 0.5 * eps0 * c * E_peak^2
las_lambda = 1.0e-6 # Laser wavelength
foc_dist = 5.0e-6 # Boundary to focal point distance
end:constant
begin:constant
las_k = 2.0 * pi / las_lambda
w0 = I_fwhm / sqrt(2.0 * loge(2.0)) # Beam Waist
ray_rang = pi * w0^2 / las_lambda # Rayleigh range
w_boundary = w0 * sqrt(1.0 + (foc_dist/ray_rang)^2) # Waist on boundary
I_boundary = I_peak_Wcm2 * (w0 / w_boundary)^2 # Intens. on boundary
rad_curve = foc_dist * (1.0 + (ray_rang/foc_dist)^2) # Boundary curv. rad.
gouy = atan(-foc_dist/rad_curve) # Boundary Gouy shift
end:constant
begin:laser
boundary = x_min
intensity_w_cm2 = I_boundary
lambda = las_lambda
phase = las_k * y^2 / (2.0 * rad_curve) - gouy
profile = gauss(y, 0, w_boundary)
end:laser
begin:output
name = o1
dt_snapshot = 10 * femto
poynt_flux = always
end:output
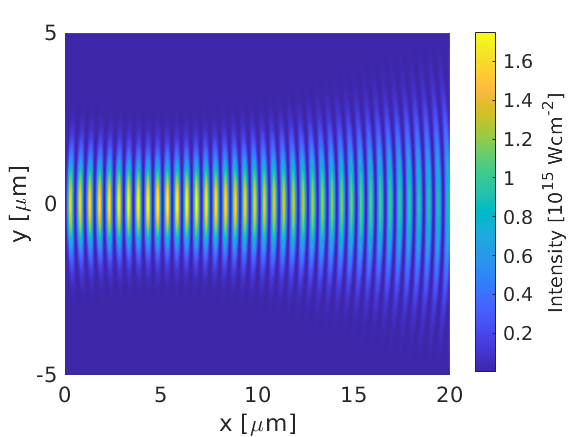
In this example, EPOCH correctly reproduces the focal point position, laser wavelength, and radial FWHM at the focus - however, the peak intensity is only $0.88\times 10^{15} \text{ Wcm}^{-2}$. This intensity reduction from target is due to the tight focal spot, with $w_0\approx 1.7$ μm being close to $\lambda = 1.0$ μm.
The deck is based on the laser test deck supplied with EPOCH, with a modified laser and longer runtime. Other classes of beam (Bessel etc) can be created similarly.