Basic examples
In this section we outline a few worked examples of setting up problems using the EPOCH input deck.
Electron two stream instability
An obvious simple test problem to do with EPOCH is the electron two stream instability. An example of a nice dramatic two stream instability can be obtained using EPOCH1D by setting the code with the following input deck file:
begin:control
nx = 400
# Size of domain
x_min = 0
x_max = 5.0e5
# Final time of simulation
t_end = 1.5e-1
stdout_frequency = 400
end:control
begin:boundaries
bc_x_min = periodic
bc_x_max = periodic
end:boundaries
begin:constant
drift_p = 2.5e-24
temp = 273
dens = 10
end:constant
begin:species
# Rightwards travelling electrons
name = Right
charge = -1
mass = 1.0
temp = temp
drift_x = drift_p
number_density = dens
npart = 4 * nx
end:species
begin:species
# Leftwards travelling electrons
name = Left
charge = -1
mass = 1.0
temp = temp
drift_x = -drift_p
number_density = dens
npart = 4 * nx
end:species
begin:output
# Number of timesteps between output dumps
dt_snapshot = 1.5e-3
# Properties at particle positions
particles = always
px = always
# Properties on grid
grid = always
ex = always
ey = always
ez = always
bx = always
by = always
bz = always
jx = always
ekbar = always
mass_density = never + species
charge_density = always
number_density = always + species
temperature = always + species
end:output
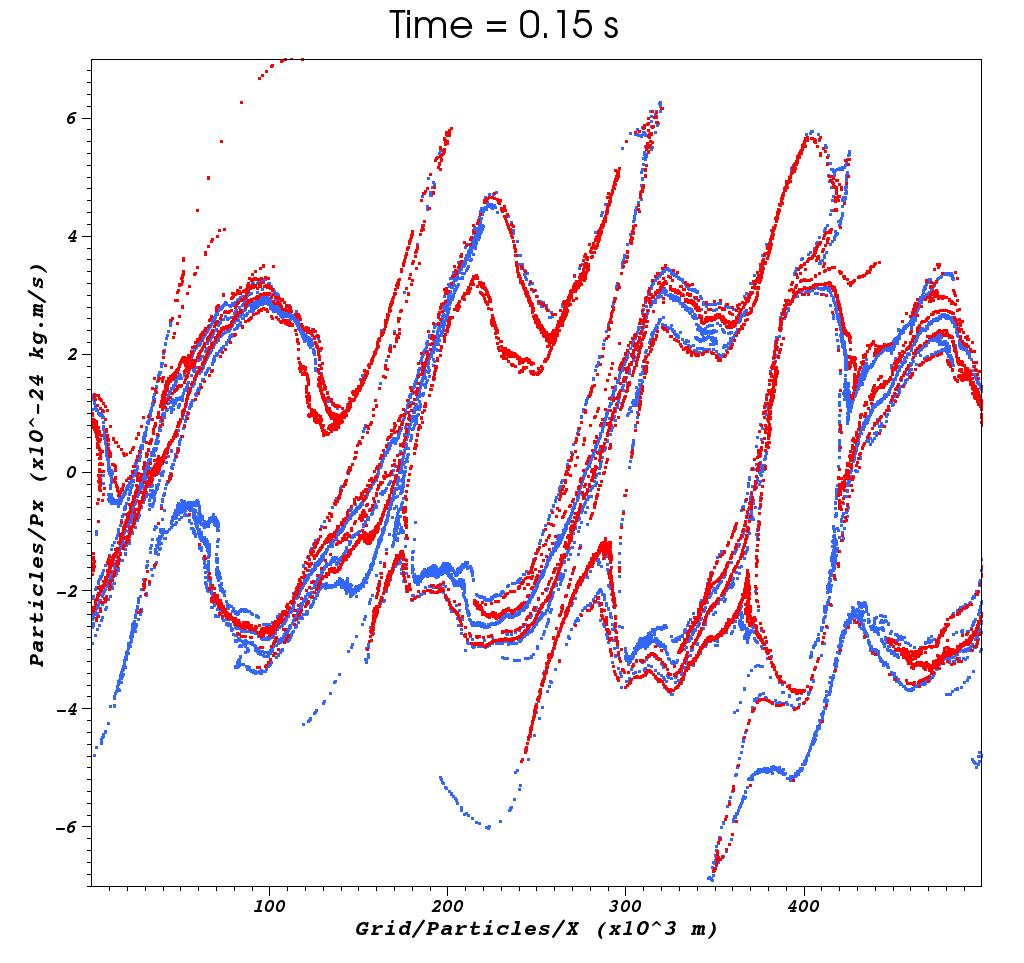 In this example, the constant block sets up constants for the momentum
space drift, the temperature and the electron number density. The two
species blocks set up the two drifting Maxwellian distributions and the
constant density profile. The final output from this simulation is shown
in the figure.
In this example, the constant block sets up constants for the momentum
space drift, the temperature and the electron number density. The two
species blocks set up the two drifting Maxwellian distributions and the
constant density profile. The final output from this simulation is shown
in the figure.
Structured density profile in EPOCH2D
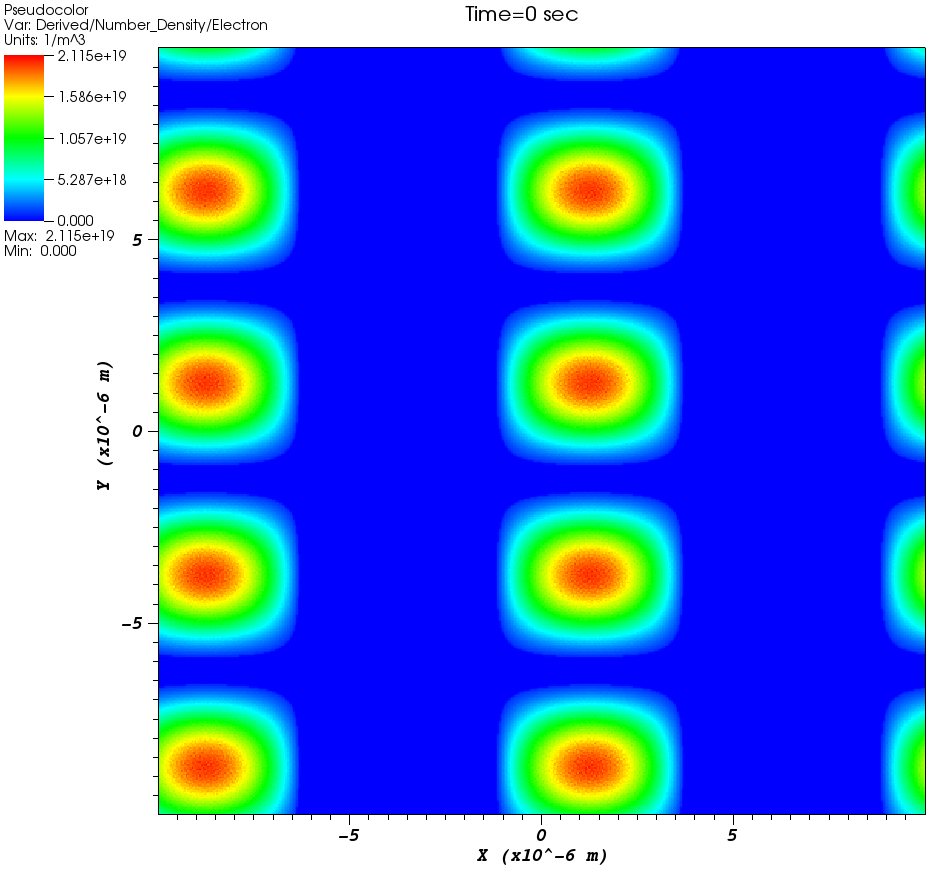
A simple but useful example for EPOCH2D is to have a highly structured initial condition to show that this is still easy to implement in EPOCH. A good example initial condition would be:
begin:control
nx = 500
ny = nx
x_min = -10 * micron
x_max = -x_min
y_min = x_min
y_max = x_max
nsteps = 0
end:control
begin:boundaries
bc_x_min = periodic
bc_x_max = periodic
bc_y_min = periodic
bc_y_max = periodic
end:boundaries
begin:constant
den_peak = 1.0e19
end:constant
begin:species
name = Electron
number_density = den_peak * (sin(4.0 * pi * x / length_x + pi / 4)) \
* (sin(8.0 * pi * y / length_y) + 1)
number_density_min = 0.1 * den_peak
charge = -1.0
mass = 1.0
npart = 20 * nx * ny
end:species
begin:species
name = Proton
number_density = number_density(Electron)
charge = 1.0
mass = 1836.2
npart = 20 * nx * ny
end:species
begin:output
number_density = always + species
end:output
The species block for Electron is specified first, setting up the electron density to be a structured 2D sinusoidal profile. The species block for Proton is then set to match the density of Electron, enforcing charge neutrality. On its own this initial condition does nothing and so only needs to run for 0 timesteps (nsteps = 0 in input.deck). The resulting electron number density should look like the figure.
A hollow cone in 3D
A more useful example of an initial condition is to create a hollow cone. This is easy to do in both 2D and 3D, but is presented here in 3D form.
begin:control
nx = 250
ny = nx
nz = nx
x_min = -10 * micron
x_max = -x_min
y_min = x_min
y_max = x_max
z_min = x_min
z_max = x_max
nsteps = 0
end:control
begin:boundaries
bc_x_min = simple_laser
bc_x_max = simple_outflow
bc_y_min = periodic
bc_y_max = periodic
bc_z_min = periodic
bc_z_max = periodic
end:boundaries
begin:output
number_density = always + species
end:output
begin:constant
den_cone = 1.0e22
ri = abs(x - 5.0e-6) - 0.5e-6
ro = abs(x - 5.0e-6) + 0.5e-6
xi = 3.0e-6 - 0.5e-6
xo = 3.0e-6 + 0.5e-6
r = sqrt(y^2 + z^2)
end:constant
begin:species
name = proton
charge = 1.0
mass = 1836.2
number_density = if((r gt ri) and (r lt ro), den_cone, 0.0)
number_density = if((x gt xi) and (x lt xo) and (r lt ri), \
den_cone, number_density(proton))
number_density = if(x gt xo, 0.0, number_density(proton))
npart = nx * ny * nz
end:species
begin:species
name = electron
charge = -1.0
mass = 1.0
number_density = number_density(proton)
npart = nx * ny * nz
end:species
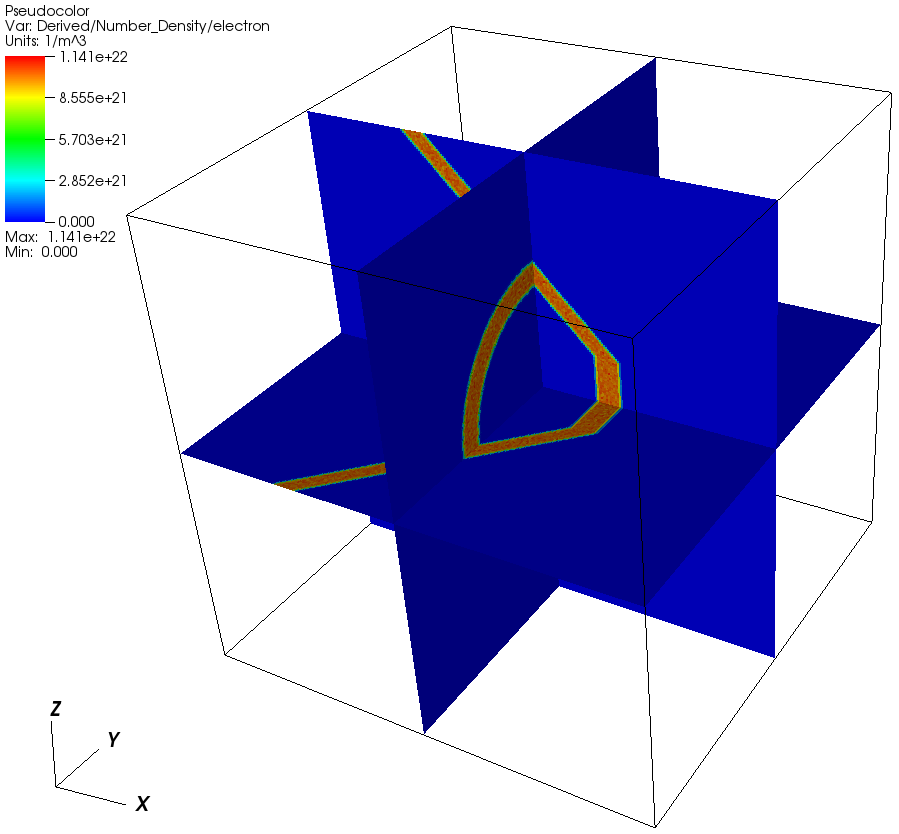
Cone initial conditions in 3D
Cone initial conditions in 2D
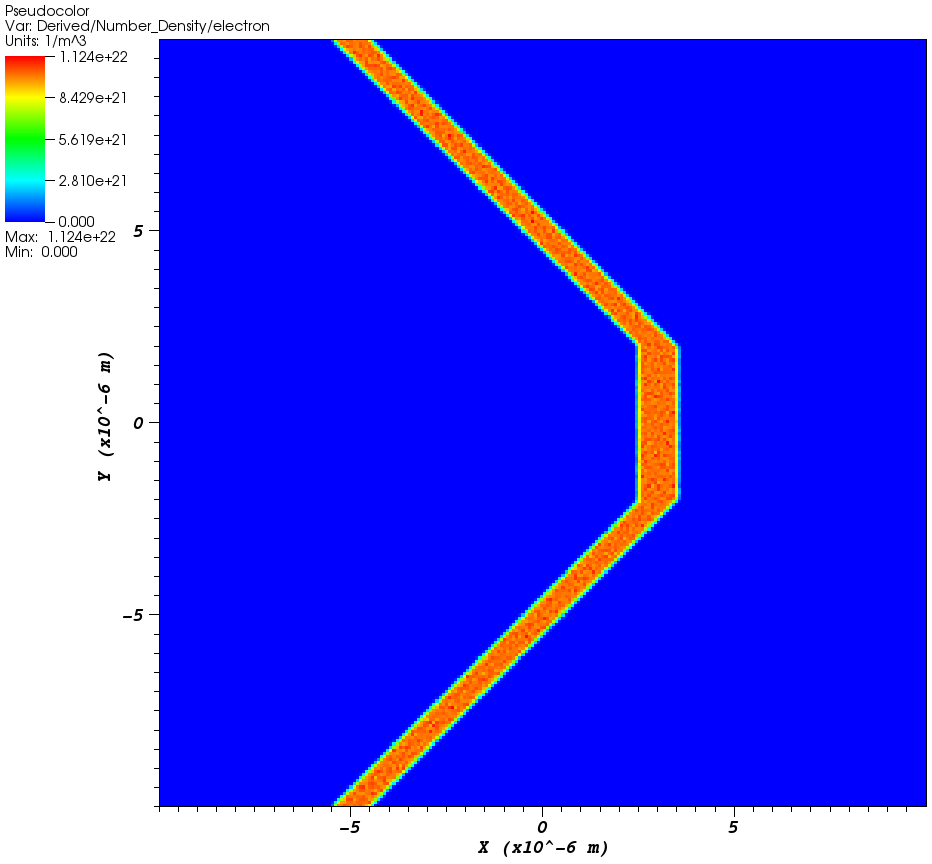
To convert this to 2D, simply replace the line r = sqrt(y^2+z^2) with
the line r = abs(y). The actual work in these initial conditions is
done by the three lines inside the block for the Proton species.
Each of these lines performs a very specific function:
- Creates the outer cone. Simply tests whether r is within the range of radii which corresponds to the thickness of the cone and if so fills it with the given density. Since the inner radius is x dependent this produces a cone rather than a cylinder. On its own, this line produces a pair of cones joined at the tip.
- Creates the solid tip of the cone. This line just tests whether the point in space is within the outer radius of the cone and within a given range in x, and fills it with the given density if true.
- Cuts off all of the cone beyond the solid tip. Simply tests if x is greater than the end of the cone tip and sets the density to zero if so.
This deck produces an initial condition as in the Figures in 3D and 2D respectively.