Using delta f

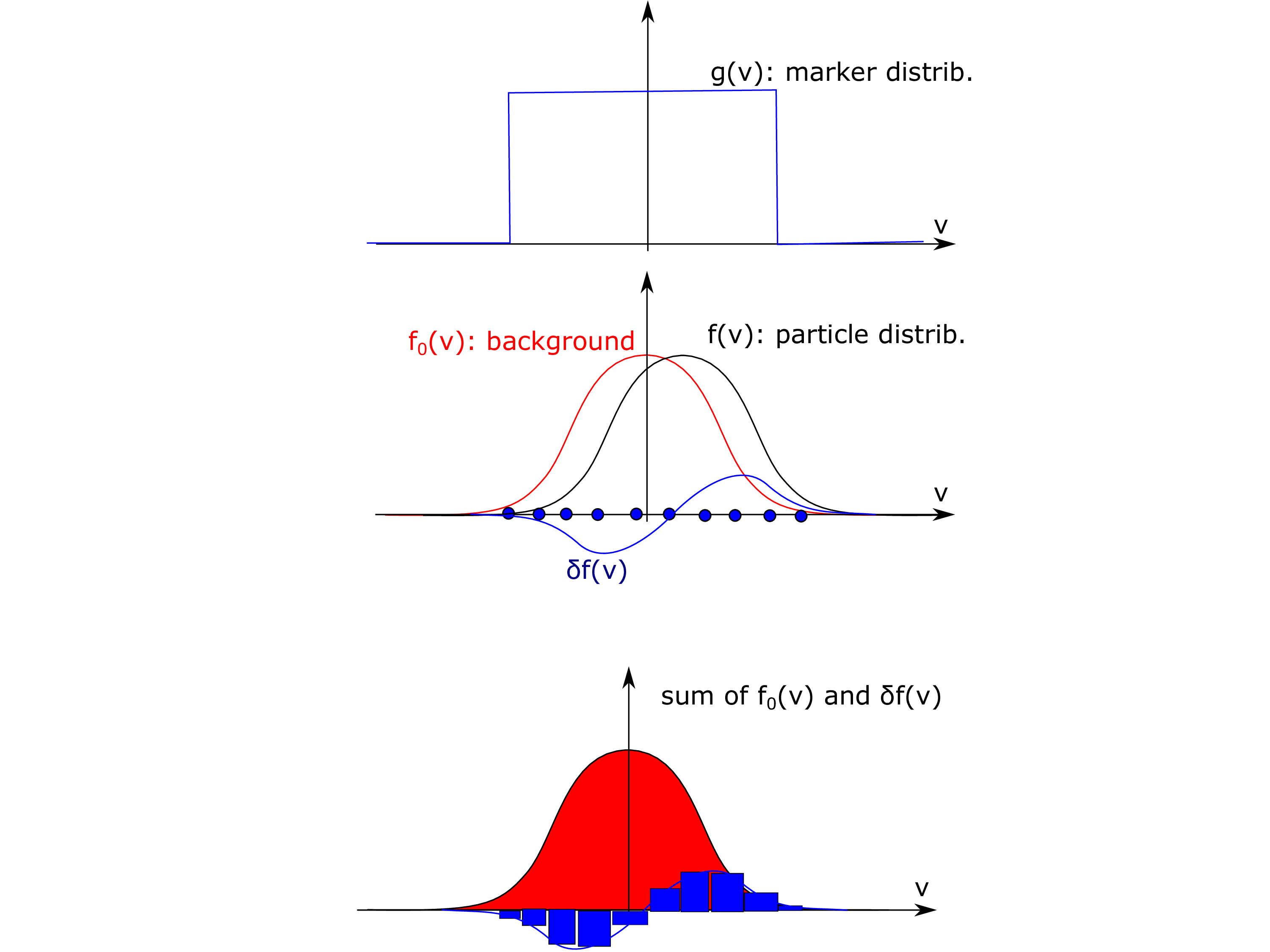
To help reduce the impact of numerical noise in certain simulations, the delta-f method may be used in for specified particle species. The delta-f method effectively subtracts a background distribution $f_0$ when calculating currents due to the motion of markers; when the particle distribution function $f$ is close to $f_0$, this substantially reduces the statistical noise in the currents. Only current deposition is implemented differently, and the equations of motion of the markers are not modified in this delta-f approach.

The component of the currents associated with the background $f_0$ may in principle be calculated analytically, but the delta-f implementation in EPOCH assumes (but does not check) that the total background current is zero.

In order to use the delta-f method EPOCH must be compiled with the #DELTAF_METHOD precompiler flag enabled. Standard input simulations are not affected by switching on this flag, but the user may then choose to treat certain species in the plasma using the delta-f method. To enable delta-f calculation for a species the background distribution function $f_0$ must be defined in the input block. $f_0$ is specified using variables similar to those used to specify $f$. The current implementation of delta-f allows only a spatially uniform drifting Maxwellian $f_0$, with temperatures $T_x$, $T_y$ and $T_z$ allowed to differ from each other. In 3D, for the case where the temperature in each direction is equal, we have $f_0=n_0(2\pi T{)}^{-3/2}\exp \left(\frac{m(\mathbf{v}-{\mathbf{v}}_{\mathbf{d}}{)}^2}{2k_{B}T}\right).$

The parameters number_density_back, temp(x,y,z)_back and drift(x,y,z)_back in each species specification in the input deck set $f_0$. number_density_back=0 is the default and is equivalent to not using the delta-f method.

For example, the electron species component of an input deck solved using delta-f might be written:

begin:species 
   name = electron 
   charge = -1.0 
   mass = 1.0 
   frac = 0.3 
   temp = 1e8 
   temp_back = 1e8 
   number_density = 1e20 
   number_density_back = 1e20 
end:species

Additional distribution function diagnostic options are supplied for the Delta-f version. Standard diagnostics work as usual based on the total distribution function $f$ but it is also possible to output the Delta-f component of the distribution functions by adding output_deltaf = T in dist_fn components of the input deck.

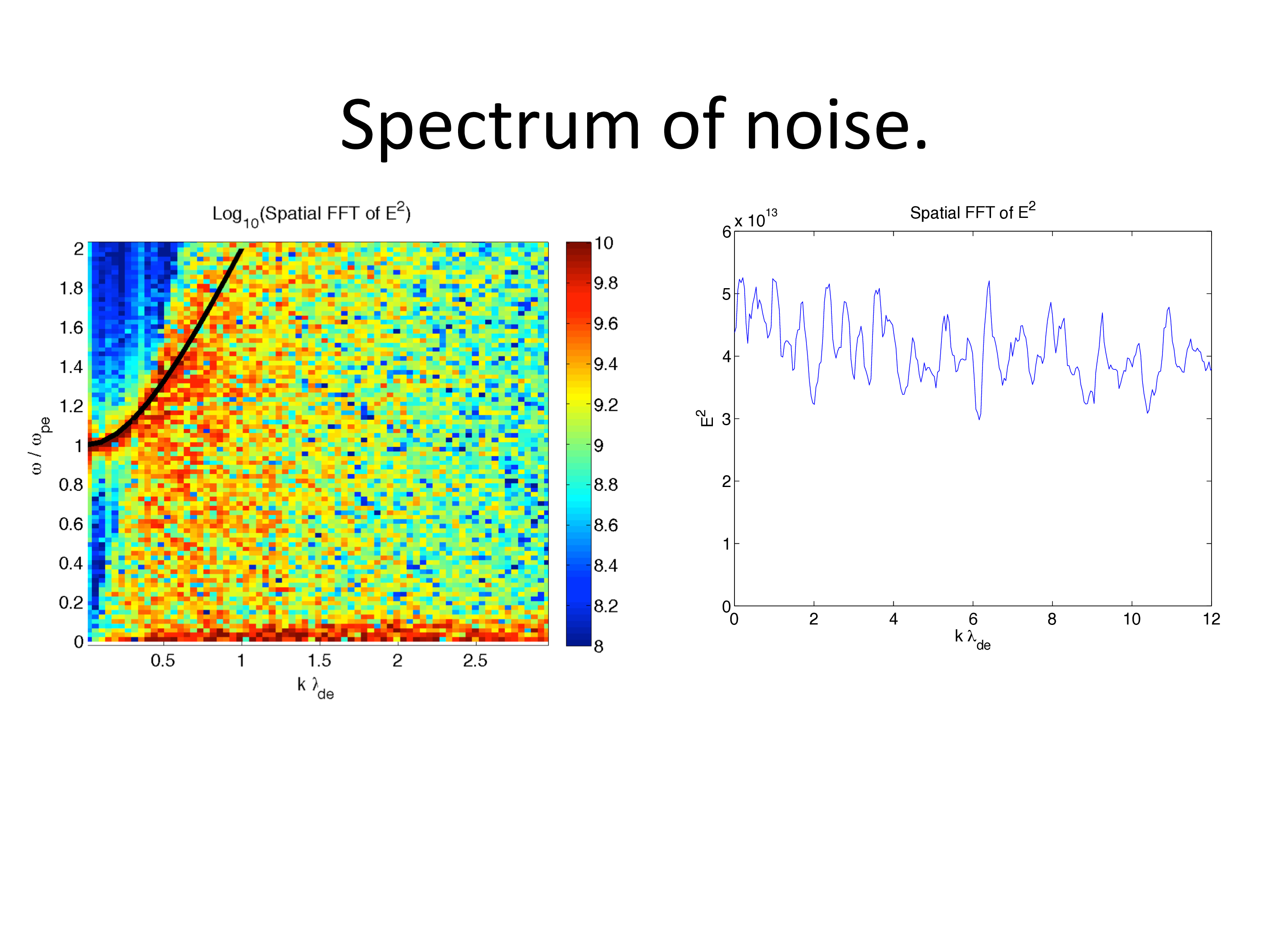
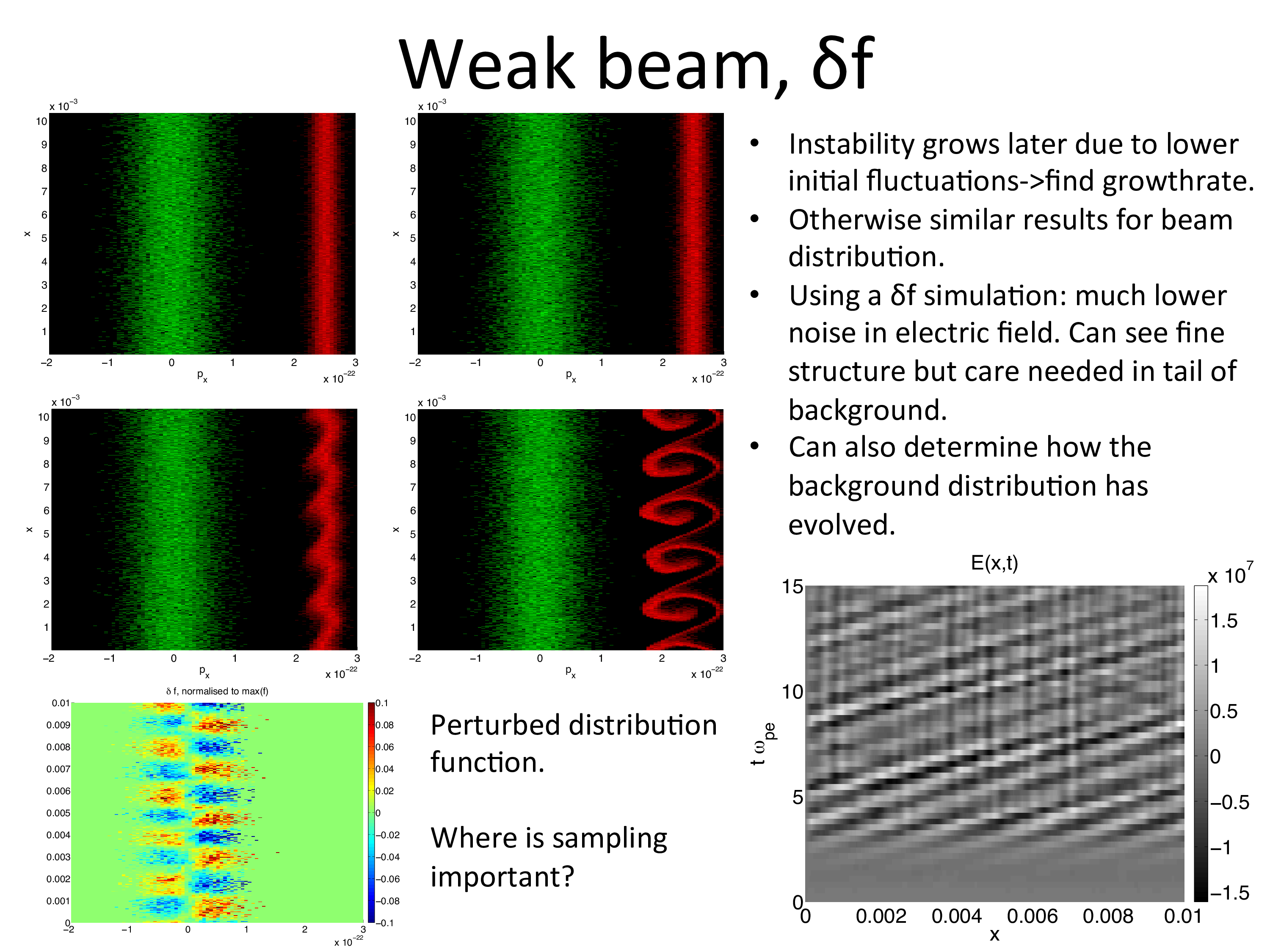
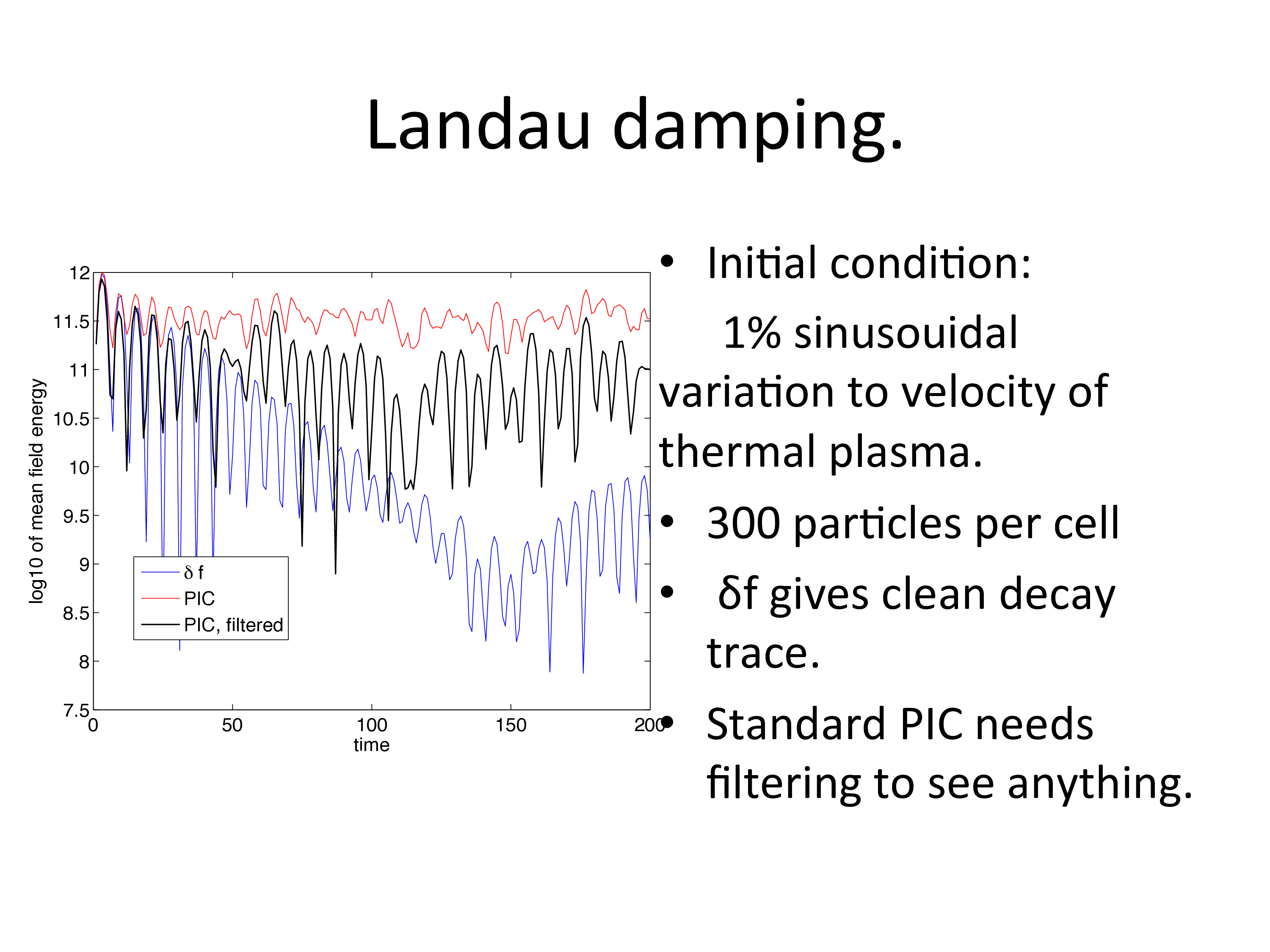
An example input deck is supplied in the 1D version as twostream_deltaf.deck. This uses the delta-f method to solve the weak-beam two stream instability. The bulk plasma species is solved using the delta-f method, since this evolves very little, and mostly supports the Langmuir waves that the weak beam interacts with. The relative change to the beam species is large, and the standard PIC method, rather than delta-f is used to model this species. A comparison of the electric field diagnostics between standard and delta-f simulations shows a substantial decrease in noise.

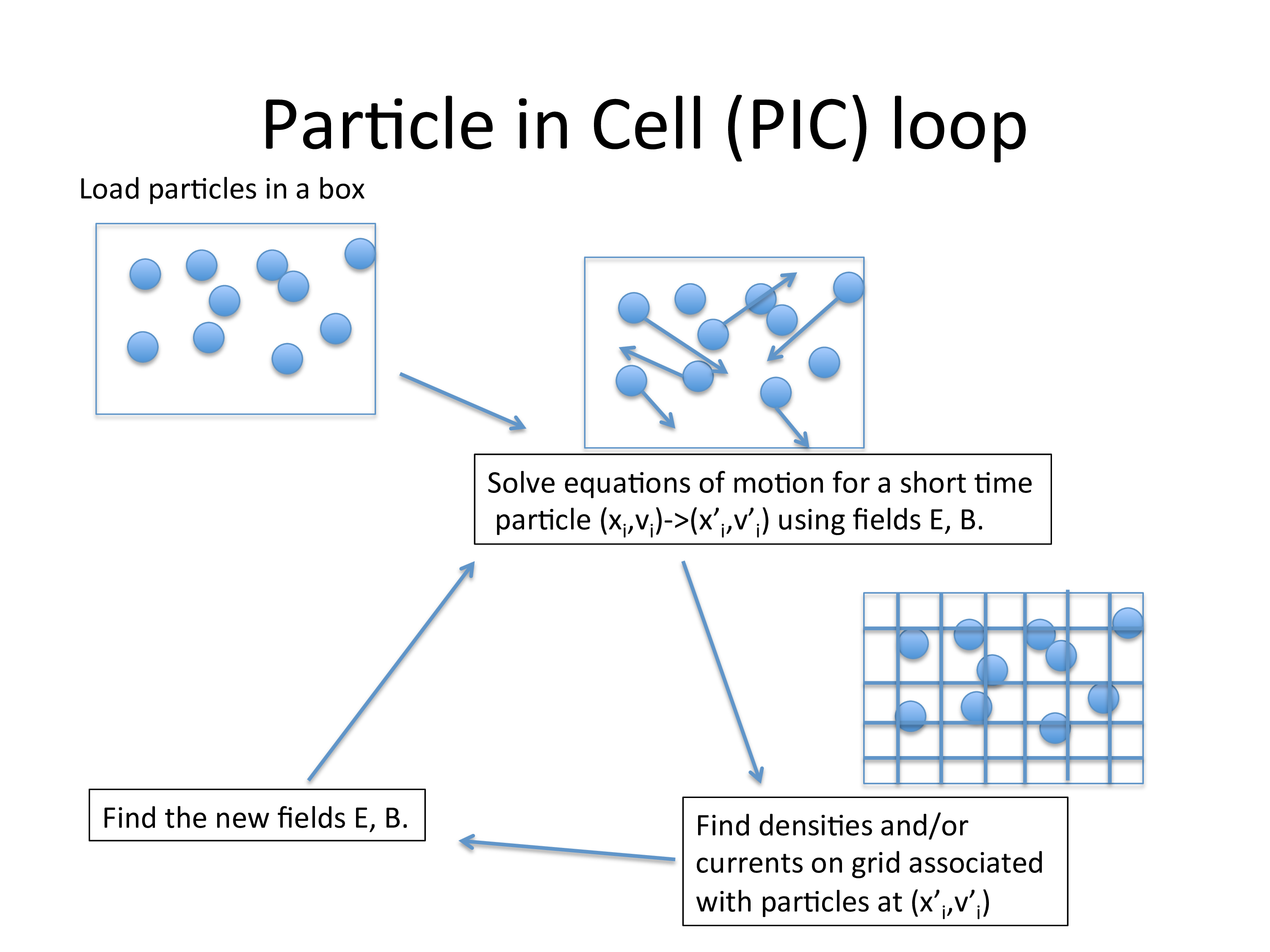
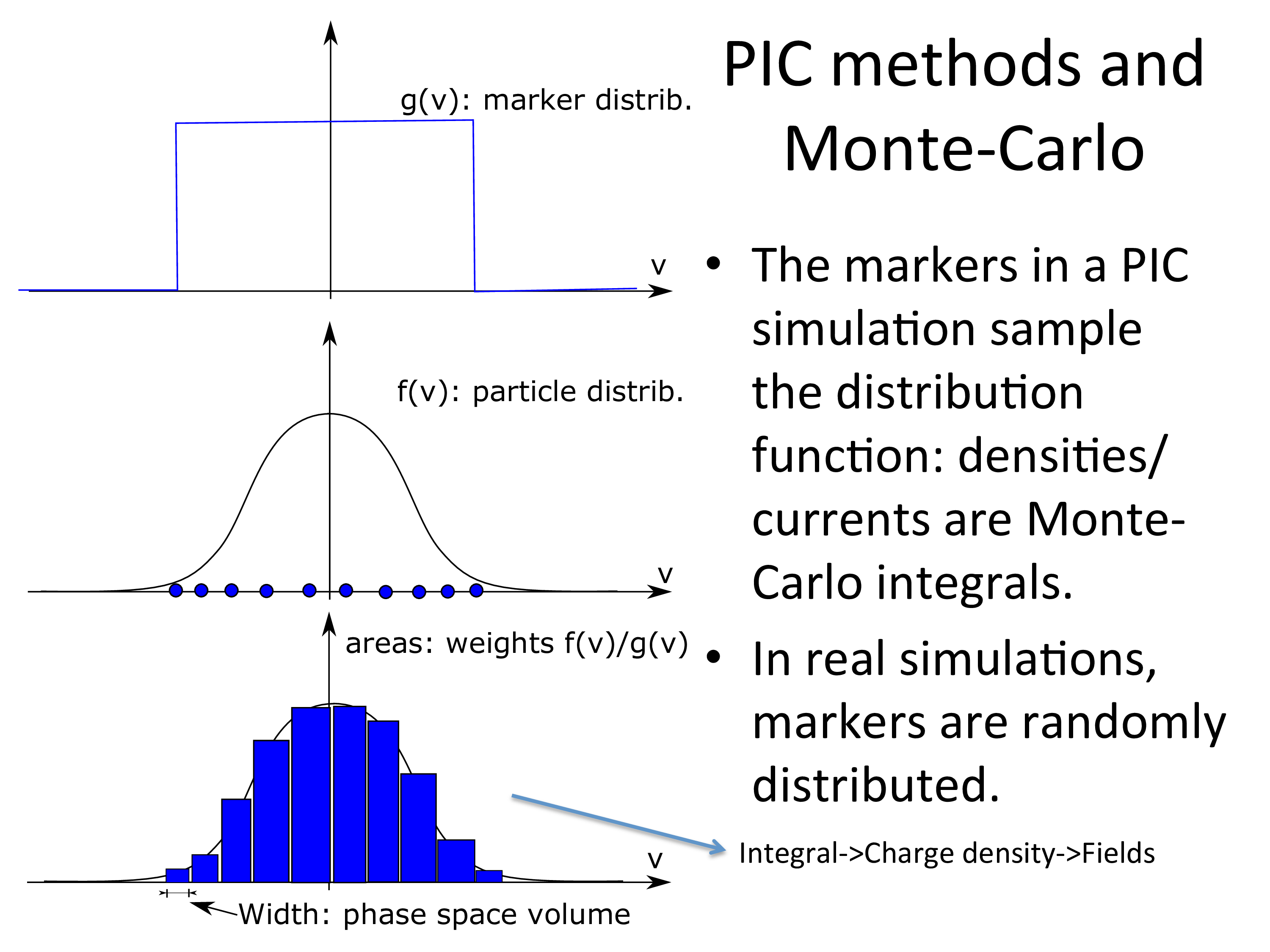
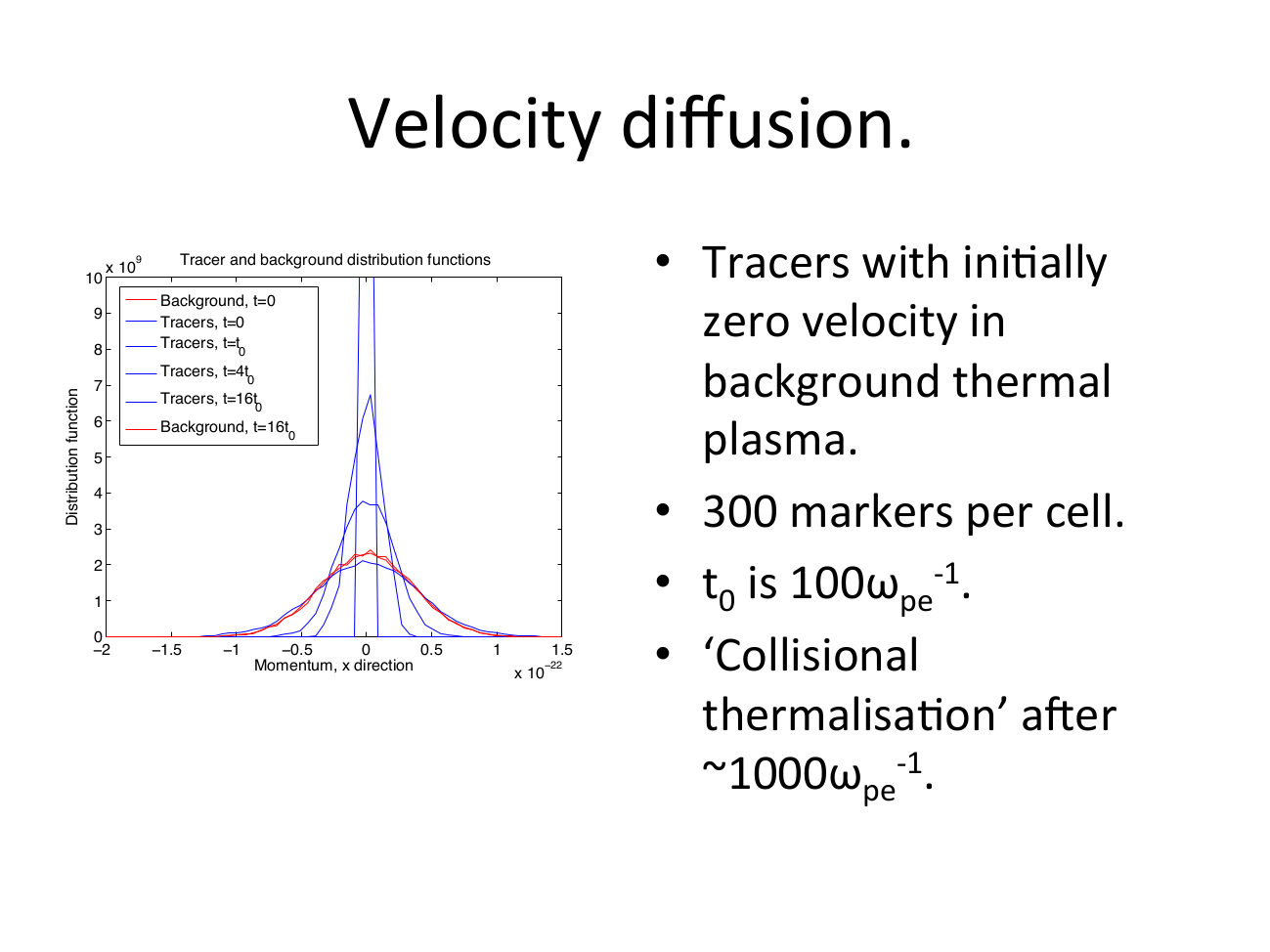
The rest of this page features slides detailing the model: